728x90
반응형
그래프 탐색 알고리즘
- 그래프에서 모든 정점을 순회하는 방법에는 크게 두가지가 있다. (DFS/BFS)
- DFS(Depth First Search) 는 '깊이 우선 탐색' 이라는 뜻으로 그래프의 정점을 방문할 때 하나의 분기를 완전히 탐색한 후 다음 분기로 넘어가는 방식이다.
- BFS(Breadth First Search) 는 '너비 우선 탐색' 이라는 뜻으로 깊이의 길이가 같은 모든 정점을 방문 한 후 다음 깊이로 넘어가서 방문할 정점이 없을 때 까지 탐색하는 방식이다.
깊이 우선 탐색(DFS)
- 깊이 우선 탐색 방식은 미로 찾기와 비슷한 방법으로 진행된다.
- 한 정점에서 시작하여 분기를 하나 선택하고 하나의 분기를 완전히 탐색하고 빠져나온다.
- 이후 다음 분기 에서도 똑같이 탐색을 진행한다.
DFS 탐색 순서

- 먼저 탐색이 완료된 곳을 저장할 배열이나 리스트를 만들어주고 해당 정점과 인접해 있는 정점들의 정보를 보관할 스택도 하나 만들어 준다.

- 0부터 시작했으니 탐색이 완료된 정점인 0을 Visited에 추가해주고 인접 정점들의 정보인 1,2,3을 Stack에 보관해 주자.

- 다음으로 한쪽 분기를 선택해 해당 분기 끝까지 탐색을 완료해야 한다.
- 1에 해당하는 정점쪽으로 탐색을 시작하고 1은 방문을 완료하였으니 Visited에 추가한다.
- 인접 정점 정보를 가지고 있는 Stack에서 1은 방문을 완료하였으니 제거한다.

- 1에 해당하는 분기에 더 이상 정점이 존재하지 않으니 다음 분기로 넘어간다.
- 2에 해당하는 정점에 대한 방문을 완료했다.
- 방문한 정점 목록에 2를 추가하고 Stack에서 2를 제거한다.
- 2 정점이 가지고 있는 인접 정점인 4에 대한 정보를 Stack에 추가한다.
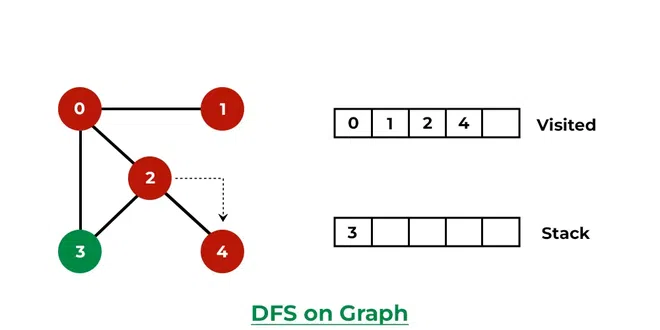
- 2번 분기에 대한 탐색을 완료해야 하니 해당 분기 안쪽으로 탐색을 계속한다.
- 2번 분기의 안쪽 정점인 4에 대한 탐색을 완료한다.
- 방문한 정점 목록에 4를 추가하고 인접 정점 정보에서 4를 제거한다.
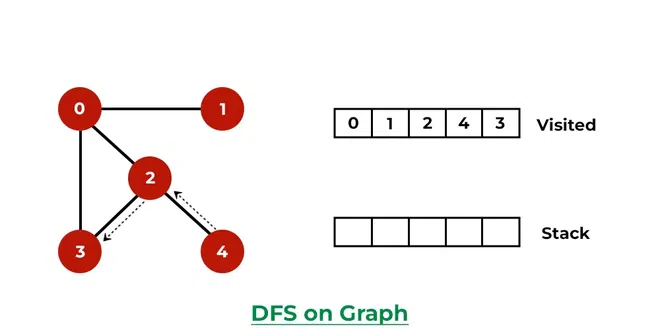
- 마지막으로 3번 정점에 대한 방문을 완료하고 인접 정점 정보에서 3을 제거하면 탐색이 완료된다.
코드 예제
C# 으로 위 예제 그래프를 DFS로 표현해보자.
public List<int> DFS(Dictionary<int, List<int>> graph, int start)
{
// 방문한 노드를 저장할 리스트
List<int> visited = new List<int>();
// 탐색할 노드를 저장할 스택
Stack<int> stack = new Stack<int>();
// 시작 노드를 스택에 추가
stack.Push(start);
while (stack.Count > 0) // 탐색한 노드를 저장할 스택에 정점이 남아 있다면 탐색을 반복
{
// 스택에서 노드를 꺼냄
int node = stack.Pop();
if (!visited.Contains(node)) // 방문할 노드를 저장할 리스트에 해당 정점인 node 값이 없다면
{
// 노드를 방문 처리
visited.Add(node);
// 인접한 노드를 스택에 추가
List<int> neighbors = graph[node];
for (int i = 0; i < neighbors.Count; i++) // 인접 노드를 반복함
{
int neighbor = neighbors[i];
if (!visited.Contains(neighbor)) // 인접 노드를 방문하지 않았다면 스택에 추가함.
{
stack.Push(neighbor);
}
}
}
}
return visited; // 방문한 노드 리스트 반환
}
- DFS를 구현하고 방문 정점 순서를 출력하는 메소드를 만든다.
- 해당 메소드에는 방문 정점 정보를 가진 리스트와 탐색할 정점 정보를 가진 스택을 하나 씩 만든다.
- 가장 먼저 시작할 정점을 스택에 추가 해 준다.
- 탐색 정보를 가진 스택의 정점 갯수 만큼 반복문을 돌린다.
- 방문한 정점의 정보를 가진 리스트에 해당 정점 값이 아직 추가되지 않았다면 해당 정점을 방문처리 해준다.
- 다음 정점에서도 인접 노드들을 반복해서 확인하고 방문하지 않은 노드가 있다면 Stack에 추가해 준다.
- 최종적으로 방문한 리스트의 목록을 반환한다.
static void Main()
{
// 그래프 정의 (인접 리스트)
Dictionary<int, List<int>> graph = new Dictionary<int, List<int>>
{
{ 0, new List<int> { 1, 2 } }, // 정점 0과 연결된 정점들
{ 1, new List<int> { 0 } }, // 정점 1과 연결된 정점들
{ 2, new List<int> { 0, 3, 4 } }, // 정점 2와 연결된 정점들
{ 3, new List<int> { 2 } }, // 정점 3과 연결된 정점들
{ 4, new List<int> { 2 } } // 정점 4와 연결된 정점들
};
// DFS 호출
List<int> visited = DFS(graph, 0);
// 방문한 노드 출력
Console.WriteLine("DFS 순서:");
for (int i = 0; i < visited.Count; i++)
{
Console.Write(visited[i] + " ");
}
}
Main문에서 그래프를 먼저 인접 리스트로 정의해주고 DFS를 호출해보자.

출력이 완료된다.
너비 우선 탐색(BFS)
- 너비 우선 탐색은 한 정점에서 시작해서 인접 정점을 탐색한다.
- 이때 탐색 순서는 깊이가 같은 모든 정점을 반복하여 탐색한 후에 다음 깊이로 들어가 다음 탐색을 진행한다.
BFS 탐색 순서

- 먼저 방문한 정점의 정보를 가진 Visited를 리스트나 배열로 구현한다.
- 너비 우선 탐색은 탐색을 도와줄 Queue가 필요하다.
- Queue는 현재 레벨(깊이)의 노드를 먼저 처리하고 다음 레벨의 노드를 나중에 처리하는 역할을 수행한다.
- 제일 먼저 0을 Queue에 넣어준다.

- 0은 방문이 완료되었으니 Visited에 추가한다.
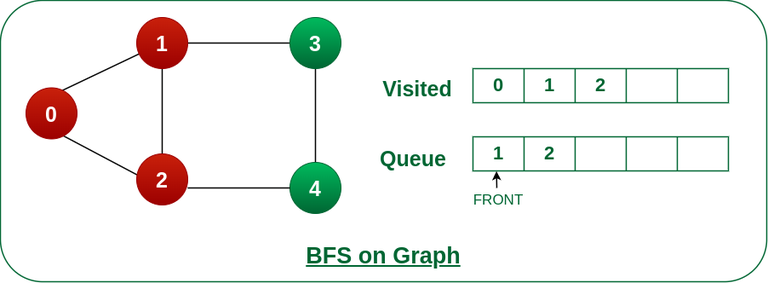
- 0과 인접한 노드인 1과 2를 방문한다.
- 방문 완료한 정점인 1과 2 역시 Queue에 추가한다.
- 방문 완료한 정점의 이전 정점은 Queue에서 제거한다 (0)
- Queue에 남아있는 정점을 조사하고 (1,2) 해당 정점의 인접 노드를 조사한다.
- 위 예제에서는 1과 2를 조사해야 한다.

- 1과 인접했던 3을 먼저 방문한다.
- 방문이 완료되면 Queue에서 해당 요소의 이전 노드를 제거한다 (1)

- 같은 레벨에 있는 남은 요소인 4를 마저 방문한다.
- 4에 대한 방문이 완료되었으니 이전 노드인 2는 Queue에서 제거한다.

- 4에 대한 탐색을 완료 했고 인접 노드인 3도 이미 방문이 완료된 노드이니 Queue에서 제거한다.
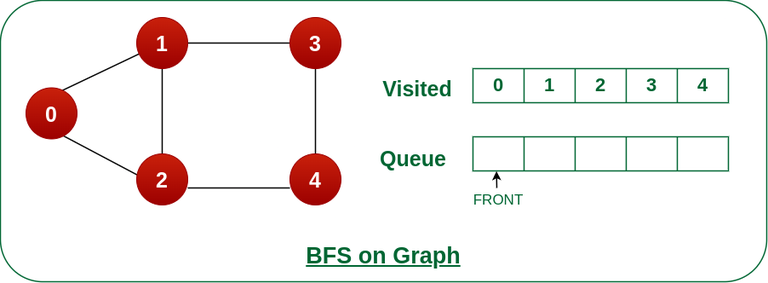
- 마지막 남은 Queue 역시 더 이상 탐색할 노드가 없으므로 Queue에서 제거한다.
- Queue가 비면 탐색이 완료된다.
코드 예제
C# 으로 위 예제 그래프를 BFS로 표현해보자.
// BFS 메소드: 주어진 그래프에서 시작 노드부터 BFS를 수행
public List<int> BFS(Dictionary<int, List<int>> graph, int start)
{
// 방문한 노드를 저장할 리스트
List<int> visited = new List<int>();
// 탐색할 노드를 저장할 큐
Queue<int> queue = new Queue<int>();
// 시작 노드를 큐에 추가하고 방문 처리
queue.Enqueue(start);
visited.Add(start);
// 큐가 비어있을 때까지 반복
while (queue.Count > 0)
{
// 큐에서 노드를 꺼냄
int node = queue.Dequeue();
// 현재 노드의 인접 노드를 큐에 추가
for (int i = 0; i < graph[node].Count; i++)
{
int neighbor = graph[node][i];
if (!visited.Contains(neighbor))
{
queue.Enqueue(neighbor);
visited.Add(neighbor);
}
}
}
// 방문한 노드 리스트 반환
return visited;
}
- BFS를 출력하고 방문 순서를 반환하는 메소드를 만든다.
- 방문 노드 정보를 저장하는 리스트 visited를 만든다.
- 탐색할 노드를 저장하는 queue를 만든다.
- 시작 노드 (0) 을 queue에 Enqueue 하고 방문 처리 후 BFS를 시작한다.
- while (queue.Count > 0): 큐가 비어있을 때까지 반복한다. (탐색할 노드가 없을 때 까지)
- 현재 노드의 인접 노드의 수만큼 탐색을 반복한다.
- 인접 노드를 방문하지 않았다면 큐에 추가하고 방문 처리한다.
static void Main()
{
// 그래프 정의 (인접 리스트)
Dictionary<int, List<int>> graph_2 = new Dictionary<int, List<int>>
{
{ 0, new List<int> { 1, 2 } },
{ 1, new List<int> { 0, 3 } },
{ 2, new List<int> { 0, 4 } },
{ 3, new List<int> { 1, 4 } },
{ 4, new List<int> { 2, 3 } }
};
// BFS 호출
List<int> visited_2 = BFS(graph_2, 0);
// 방문한 노드 출력
Console.WriteLine("BFS 방문 순서:");
for (int i = 0; i < visited_2.Count; i++)
{
Console.Write(visited_2[i] + " ");
}
}
- BFS 출력을 위한 그래프를 정의한다.
- BFS를 호출하고 해당 그래프를 넣어준다. (시작 노드는 0)

순서대로 출력이 완료된다.
정리
- DFS는 재귀와 스택을 사용하기 때문에 메모리 효율성이 우수한 그래프 탐색 방법이다.
- 하지만 항상 최단 경로를 보장하지는 않고 그래프에서 방문 처리를 꼼꼼하게 하지 않으면 무한루프에 빠질 위험성도 있다.
- 깊이가 매우 깊은 그래프에서는 스택 오버 플로우의 위험성도 존재한다.
- BFS는 최단 경로를 찾는데에 유리하고 노드를 레벨별로 탐색하기에 레벨이 계속 확장되는 탐색이 필요할 때 유리하다.
- 큐에 많은 노드를 저장해야 하기에 메모리 사용량이 높은 편이다.
- 탐색 중간마다 많은 노드들을 저장해야 하기에 공간 복잡도가 높은 편이다.
사진 출처 : https://www.geeksforgeeks.org/
728x90
반응형
'알고리즘' 카테고리의 다른 글
| 알고리즘 - 동적 계획법(Dynamic Programming) (2) | 2024.06.04 |
|---|---|
| 알고리즘 - 이진 탐색(이분 탐색) (2) | 2024.05.30 |
| 알고리즘 - 완전 탐색 기법(1) (Brute - Force) (3) | 2024.05.21 |
| 알고리즘 - 정렬(Sort) (2) | 2024.05.18 |
| 알고리즘 - 정렬의 종류 별 시간 복잡도 (1) | 2024.05.17 |
