비트를 쪼개는 개발자

allen321@naver.com

알고리즘

알고리즘 - 정렬(Sort)

MozarTnT 2024. 5. 18. 02:17
728x90
반응형

 

 

 

정렬(Sort) 이란?

 

 

  • 데이터의 집합을 특정 순서에 따라 배열하는 방법.

 

  • 데이터의 집합의 순서를 최대 값, 최소 값 등 필요한 기준에 따라 재 배열하는 행위.

 

  • 정렬에는 여러 종류의 정렬이 있고 각 정렬마다 다른 시간 복잡도와 데이터에 따라 적합한 방식의 정렬이 다르다.

 

 

 

정렬의 종류

 

 

 

 

버블 정렬 (Bubble Sort)

 

 

 

 

 

 

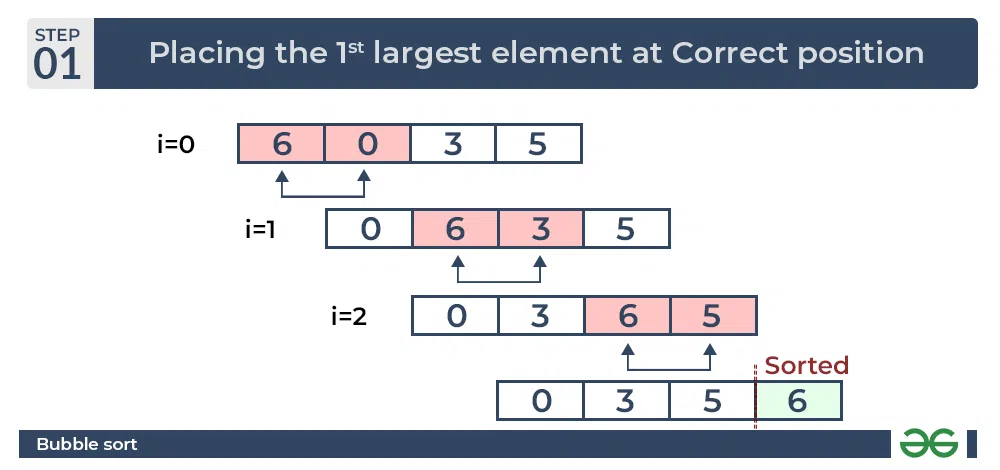
  • 인접한 두 요소를 비교하고 정렬이 필요하면 두 데이터를 교환하는 작업을 반복 하는 정렬 방식

 

  • 가장 간단하지만 시간 복잡도적인 측면에서 비효율적이다

 

  • 이미 정렬이 된 데이터도 교환하는 일이 발생하며 배열의 모든 요소에 한번씩은 접근해야 함

 

 

 

C# 예시 코드

 

 

public void BubbleSort(int[] array) // 버블 정렬 함수
{
    int n = array.Length; // 배열 길이

    for(int i = 0; i < n - 1; i ++) // 자기 자신과 비교할 필요는 없으니까 -1
    {
        for(int j = 0; j < n - 1; j++)
        {
            if (array[j] > array[j + 1])
            {
                int temp = array[j]; // 데이터 스왑
                array[j] = array[j + 1];
                array[j + 1] = temp;
            }
        }
    }
}

 

 

 

 

 

 

 

 

 

선택 정렬 (Selection Sort)

 

 

 

 

 

 

 

 

 

 

 

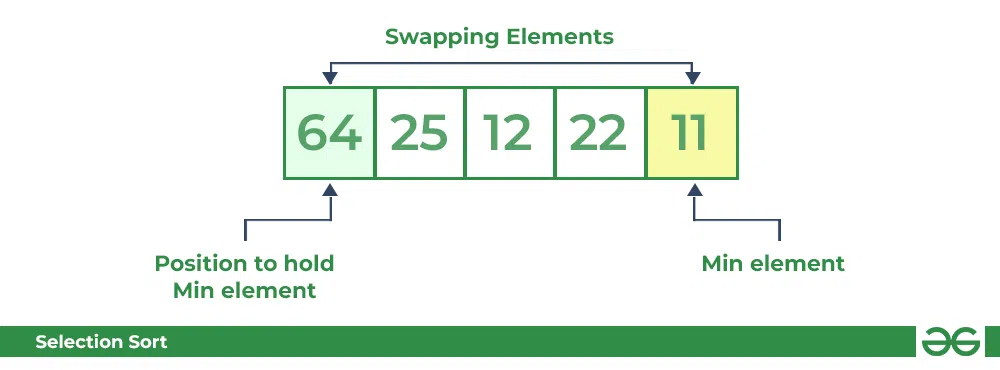
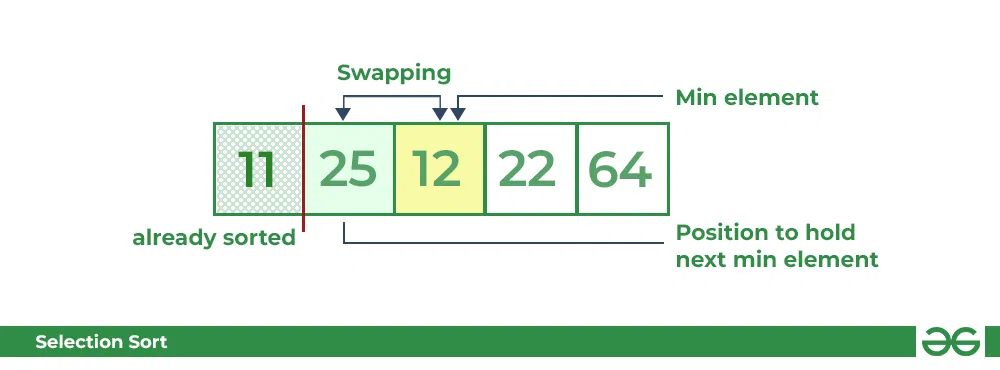
  • 배열 내에서 최소값을 찾고 맨 앞의 데이터와 교체하는 정렬 방식

 

  • 위의 순서가 수행된 데이터는 정렬된걸로 간주하고 다음 인덱스로 해당 동작을 반복한다.

 

  • 2중 for문이 사실상 강제된다. [O(N2)]

 

 

C# 예시 코드

 

public void SelectionSort(int[] array) // 선택 정렬 함수
{
    int n = array.Length; // 배열 길이

    for(int i = 0; i < n - 1; i ++) // 자기 자신과 비교할 필요는 없으니까 -1
    {
        int minNum = i; // 최소값 찾기 용 변수 i로 초기화

        for(int j = i + 1; j < n; j++) // i 다음 요소들 
        {
            if (array[j] < array[minNum]) // 해당 요소가 최소값 보다 작으면 minNum에 저장
            {
                minNum = j;
            }
        }
        int temp = array[minNum]; // 해당 최소값을 array[i] 와 교환
        array[minNum] = array[i];
        array[i] = temp;
    }
}

 

 

 

 

 

 

 

 

삽입 정렬 (Insertion Sort)

 

 

 

 

 

 

 

 

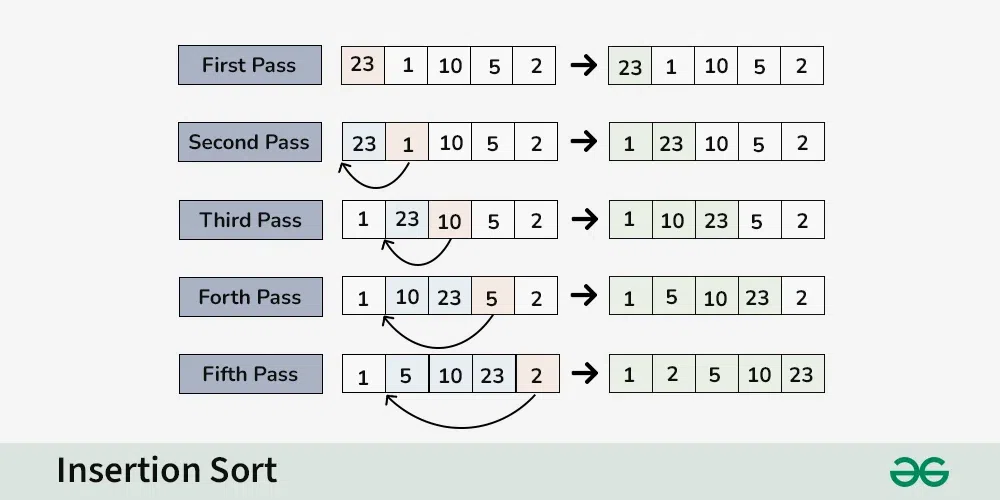
  • 새로운 원소를 이전까지 정렬시켜둔 원소 사이에 삽입시키는 정렬 방식

 

  • 2번째 인덱스부터 시작해서 이전 원소와 비교해 데이터를 기준에 맞는 위치에 넣음

 

  • 데이터 원소들이 어느정도 정렬이 된 상태에서 사용할 경우 높은 효율성을 가짐

 

  • 최선의 경우에 시간 복잡도가 O(N) 이라는 높은 효율성을 보여줌

 

 public void InsertionSort(int[] array)
 {
     int n = array.Length; // 배열 길이

     for (int i = 1; i < n; i++) // 두번째 요소 부터
     {
         int temp = array[i]; // 현재 요소 저장
         int j = i - 1;

         while (j >= 0 && array[j] > temp) // j 값은 temp 이전 값, j의 요소가 현재 요소보다 커질때 까지 이전 요소 접근
         {
             array[j + 1] = array[j];
             j = j - 1;
         }
         array[j + 1] = temp;
     }
 }

 

 

 

 

 

 

 

 

 

 

병합 정렬 (Merge Sort)

 

 

 

 

 

 

 

  • 병합 정렬은 리스트를 반으로 나누고, 나눈 배열의 인덱스가 각각 하나씩만 남을때 까지 반으로 분할하는 작업을 반복한다.

 

 

병합 정렬 순서

 

  • 하나씩 남은 배열들을 빈 배열을 만들어 기준에 따라 합쳐준다.

 

  • 10개의 데이터를 가진 배열을 일반적으로 정렬해야 한다면 O(N2)의 시간복잡도를 가지며 약 100번의 연산을 수행하지만 병합 정렬시에는 O(N * log(N)) 으로 약 10 * 3.32, 즉 33.2번 정도의 연산 횟수를 가져 비교적 효율적이다.

 

  • 데이터의 길이가 길수록 효율적이라고 볼 수 있다.

 

 

 

장단점

 

  • 빈 배열을 저장할 임시 배열이 필요한 만큼 전체 배열과 동일한 크기의 배열을 저장할 메모리와 병합 과정에서 생기는 두개의 부분 배열을 임시적으로 저장할 메모리 공간이 필요하다. 

 

 

C# 예시 코드

 public void MergeSort(int[] array, int left, int right)
 {
     if (left < right)
     {
         // 중간 인덱스를 계산
         int middle = (left + right) / 2;

         // 중간을 기준으로 왼쪽 부분과 오른쪽 부분을 재귀적으로 정렬
         MergeSort(array, left, middle);
         MergeSort(array, middle + 1, right);

         // 정렬된 두 부분을 병합
         Merge(array, left, middle, right);
     }
 }

 // 두 부분을 병합하는 함수
 public void Merge(int[] array, int left, int middle, int right)
 {
     // 두 부분의 크기를 계산
     int n1 = middle - left + 1;
     int n2 = right - middle;

     // 임시 배열 생성
     int[] leftArray = new int[n1];
     int[] rightArray = new int[n2];

     // 임시 배열에 데이터 복사
     Array.Copy(array, left, leftArray, 0, n1);
     Array.Copy(array, middle + 1, rightArray, 0, n2);

     // 임시 배열의 데이터를 병합
     int i = 0, j = 0, k = left;
     while (i < n1 && j < n2)
     {
         if (leftArray[i] <= rightArray[j])
         {
             array[k] = leftArray[i];
             i++;
         }
         else
         {
             array[k] = rightArray[j];
             j++;
         }
         k++;
     }

     // 남아 있는 요소를 복사
     while (i < n1)
     {
         array[k] = leftArray[i];
         i++;
         k++;
     }
     while (j < n2)
     {
         array[k] = rightArray[j];
         j++;
         k++;
     }
 }

 

 

 

 

 

 

 

 

 

 

 

퀵 정렬 (Quick Sort)

 

 

 

퀵 정렬(Quick Sort)은 병합 정렬(Merge Sort)과 마찬가지로 분할 알고리즘을 기반으로 하는 정렬 알고리즘임.

 

 

 

퀵 정렬 순서

 

  • 리스트에서 피벗(기준 데이터)을 설정한다.

 

  • 해당 피벗을 기준으로 피벗보다 작은 데이터는 왼쪽, 큰 데이터는 오른쪽에 배치한다.

 

  • 배열을 피벗을 기준으로 두개의 배열로 분할한다.

 

  • 나눠진 두 개의 배열에서 새로운 피벗을 선정하고 위의 과정을 반복한다.

 

 

 

장단점

  • 퀵 정렬은 피벗 선정 기준에 따라 시간복잡도가 변한다. 
  • 최악의 경우에는 O(N2)의 시간복잡도를 보여주지만 평균적으로는 O(N * log(N)) 의 시간복잡도를 가진다.
  • 구현이 간단한 편이고 추가적인 메모리 공간이 거의 필요하지 않다는 장점이 있다.

 

 

 

C# 예시 코드

 // 퀵 정렬 함수
 public void QuickSort(int[] array, int left, int right)
 {
     if (left < right)
     {
         // 피벗을 기준으로 배열을 분할
         int pivotIndex = Partition(array, left, right);

         // 분할된 왼쪽 부분을 재귀적으로 정렬
         QuickSort(array, left, pivotIndex - 1);
         // 분할된 오른쪽 부분을 재귀적으로 정렬
         QuickSort(array, pivotIndex + 1, right);
     }
 }

 // 피벗을 기준으로 배열을 분할하는 함수
 public int Partition(int[] array, int left, int right)
 {
     int pivot = array[right]; // 배열의 마지막 요소를 피벗으로 선택
     int i = left - 1; // 작은 요소들의 끝 인덱스

     for (int j = left; j < right; j++)
     {
         // 현재 요소가 피벗보다 작거나 같은 경우
         if (array[j] <= pivot)
         {
             i++;
             // 작은 요소들과 현재 요소를 교환
             int temp = array[i];
             array[i] = array[j];
             array[j] = temp;
         }
     }

     // 피벗을 올바른 위치로 이동
     int temp1 = array[i + 1];
     array[i + 1] = array[right];
     array[right] = temp1;

     return i + 1; // 피벗의 위치를 반환
 }

 

 

 

 

 

 

 

 

 

힙 정렬 (Heap Sort)

 

 

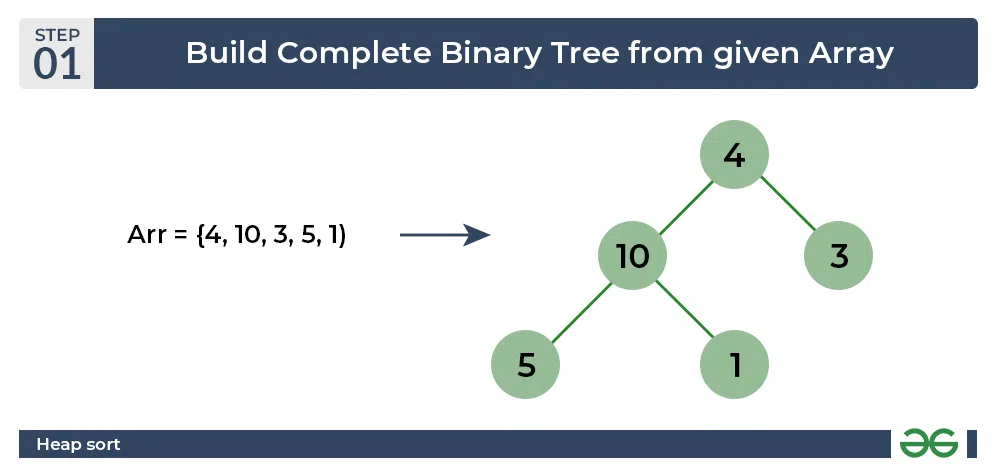
자세한 힙 정렬 순서 : https://www.geeksforgeeks.org/heap-sort/?ref=header_search

 

 

  • 완전 이진 트리 구조인 힙(Heap)을 이용해 데이터를 정렬하는 방법

 

  • 힙은 최대 힙과 최소 힙으로 구성할 수 있지만 보통은 최대 힙을 사용하여 정렬함

 

  • 힙 정렬을 노드 삭제와 힙 재구조화의 반복임

 

 

힙 정렬 순서

 

 

  • 먼저 배열을 최대 힙으로 변환 한다 (완전 이진트리 구조) 

 

  • 해당 최대 힙의 루트 노드(최댓값) 을 배열의 끝으로 이동시키고, 루트 노드는 트리의 마지막 요소와 자리를 바꾼 뒤 힙의 크기를 하나 감소시킨다.

 

  • 바뀐 힙을 최대 힙으로 다시 재 구조화 한뒤 위 과정을 반복한다.

 

 

 

장단점

 

  • 시간 복잡도가 최선, 평균, 최악 모두 O(N * log(N)) 이라는 장점이 있음.
  • 같은 값을 가진 데이터의 경우 순서가 유지되지 않아 상대적으로 불안정함.
  • 힙을 재구조화하는 과정이 반복되서 구조가 복잡한 편임.

 

 

C# 예시 코드

public void HeapSort(int[] array)
{
    int n = array.Length;

    // 배열을 힙 구조로 변환 (최대 힙 구성)
    for (int i = n / 2 - 1; i >= 0; i--)
    {
        Heapify(array, n, i);
    }

    // 하나씩 힙에서 요소를 제거하고 정렬
    for (int i = n - 1; i > 0; i--)
    {
        // 현재 루트(최대값)를 끝으로 이동
        int temp = array[0];
        array[0] = array[i];
        array[i] = temp;

        // 힙의 크기를 줄이고 루트에서 힙 구조를 재정렬
        Heapify(array, i, 0);
    }
}

// 힙을 재구성하는 함수
public void Heapify(int[] array, int n, int i)
{
    int largest = i; // 루트를 가장 큰 값으로 가정
    int left = 2 * i + 1; // 왼쪽 자식 노드
    int right = 2 * i + 2; // 오른쪽 자식 노드

    // 왼쪽 자식 노드가 루트보다 크면 왼쪽 자식을 가장 큰 값으로 설정
    if (left < n && array[left] > array[largest])
    {
        largest = left;
    }

    // 오른쪽 자식 노드가 현재 가장 큰 값보다 크면 오른쪽 자식을 가장 큰 값으로 설정
    if (right < n && array[right] > array[largest])
    {
        largest = right;
    }

    // 가장 큰 값이 루트가 아니라면 교환하고 재귀적으로 힙을 재구성
    if (largest != i)
    {
        int swap = array[i];
        array[i] = array[largest];
        array[largest] = swap;

        // 재귀적으로 영향을 받은 하위 트리를 힙으로 재구성
        Heapify(array, n, largest);
    }
}
728x90
반응형

'알고리즘' 카테고리의 다른 글

알고리즘 - 이진 탐색(이분 탐색)  (0) 2024.05.30
알고리즘 - 그래프 탐색 알고리즘 (DFS / BFS)  (0) 2024.05.27
알고리즘 - 완전 탐색 기법(1) (Brute - Force)  (0) 2024.05.21
알고리즘 - 정렬의 종류 별 시간 복잡도  (0) 2024.05.17
시간복잡도(Time Complexity) 란 ?  (0) 2024.05.07

'알고리즘'의 다른글

  • 현재글알고리즘 - 정렬(Sort)

관련글

티스토리툴바