728x90
반응형

문제 설명
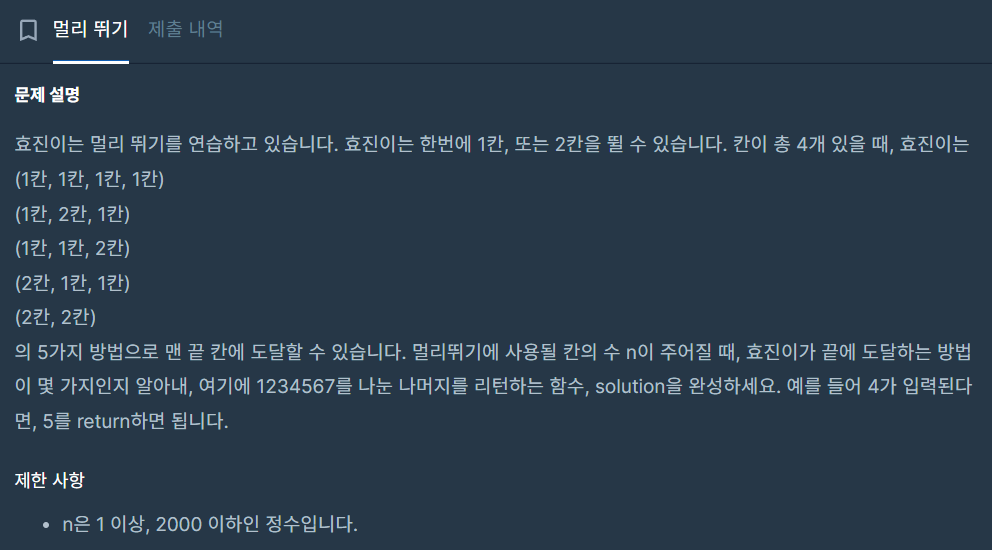
- 효진이는 한 번에 1칸 혹은 2칸을 점프 할 수 있음
- n개의 칸이 주어졌고, 마지막 칸에 도달할 때 발생하는 경우의 수를 따져야 함
- 결과로 나온 값에 1234567로 나눈 나머지 값을 return하는 함수를 완성해야 함
문제의 요지 자체는 간단하지만 오버플로우와 경우의 수가 많아지기 쉬운 케이스라고 생각했다.
문제를 풀다보니 칸 수가 증가하면서 늘어나는 값이 피보나치 수열과 거의 흡사하다는 것을 발견했고 이와 비슷하게 문제를 풀어냈다.
더보기
n=1: 1가지
[1]
n=2: 2가지
[1,1]
[2]
n=3: 3가지
[1,1,1]
[1,2]
[2,1]
n=4: 5가지
[1,1,1,1]
[1,1,2]
[1,2,1]
[2,1,1]
[2,2]
n=5: 8가지
[1,1,1,1,1]
[1,1,1,2]
[1,1,2,1]
[1,2,1,1]
[2,1,1,1]
[2,2,1]
[2,1,2]
[1,2,2]
n의 갯수가 늘어나면서 생겨나는 경우의 수가 피보나치 수열의 첫번째 수를 제외한 값과 일치하게 늘어났고 그 이유는 이전의 경우의 수에서 발생하는 경우에서 선형적으로 증가해 나가기 때문인 것 같았다.
다만 1234567로 나눈 나머지를 구하라는 이유는 피보나치 수열의 경우 큰 수를 덧셈하면서 스택 오버플로우가 발생하기 쉬운데 이를 방지하고 메모리를 효율적으로 구하기 위해서라고 생각했다.
해당 코드
public class Solution
{
public long solution(int n)
{
// 1칸이나 2칸인 경우는 바로 반환
if (n <= 2) return n;
// oneBefore: 1칸 전까지의 방법 수
// twoBefore: 2칸 전까지의 방법 수
// current: 현재 위치까지의 방법 수
long oneBefore = 1; // 1칸일 때의 방법 수로 초기화
long twoBefore = 2; // 2칸일 때의 방법 수로 초기화
long current = 0; // 현재 계산할 위치의 방법 수
// 3부터 n까지 반복하면서 각 위치에서의 방법 수 계산
for (int i = 3; i <= n; i++)
{
// 현재 위치의 방법 수 = (1칸 전 방법 수 + 2칸 전 방법 수) % 1234567
current = (oneBefore + twoBefore) % 1234567;
// 다음 계산을 위해 값들을 한 칸씩 이동
oneBefore = twoBefore; // 이전의 twoBefore가 새로운 oneBefore가 됨
twoBefore = current; // 현재 계산한 값이 새로운 twoBefore가 됨
}
return current; // 최종 계산된 방법 수 반환
}
}

728x90
반응형
'코딩테스트' 카테고리의 다른 글
| C# [프로그래머스] 모음사전 (0) | 2024.12.09 |
|---|---|
| C# [프로그래머스] PCCP 기출문제 - 동영상 재생기 (0) | 2024.11.11 |
| C# [HackerRank] Algorithm(Data Structures) - Equal Stacks (1) | 2024.10.14 |
| C# [프로그래머스] Lv.2 괄호 회전하기 (1) | 2024.09.16 |
| C# [HackerRank] Algorithm(Data Structures) - Counting Valleys (0) | 2024.09.11 |
